Met de programmamodule Niet-lineaire dynamica kunt u de chaotische aard van de hartslag, fluctuaties in het opnameproces, fractal, zelf-vergelijkbare structuur van het ECG-signaal bestuderen.

Module bevat 4 tabbladen

1 Faseafbeelding

Een dynamisch chaosogram is een meetkunde van punten in het fasevlak waarvan de Coördinaten zijn stappen van naburige cardio-intervallen. Bij het analyseren van de gegevens, is het raadzaam om aandacht te besteden aan de vorm van het chaosogram en de verdeling van de lijnen onder de hellingshoeken.

Een gezond persoon wordt gekenmerkt door stabiele ellipsoïdale cycli met een enkele punt van aantrekking en spinachtige chaosogrammen. Wanneer de sympathoadrenale de regelafdeling wordt geactiveerd, de grootte van zo’n ellips neemt af. Op Integendeel, wanneer vagale regulatie dominant is, neemt het toe. Het punt van Attractie blijft behouden.

 

 

 

 

 

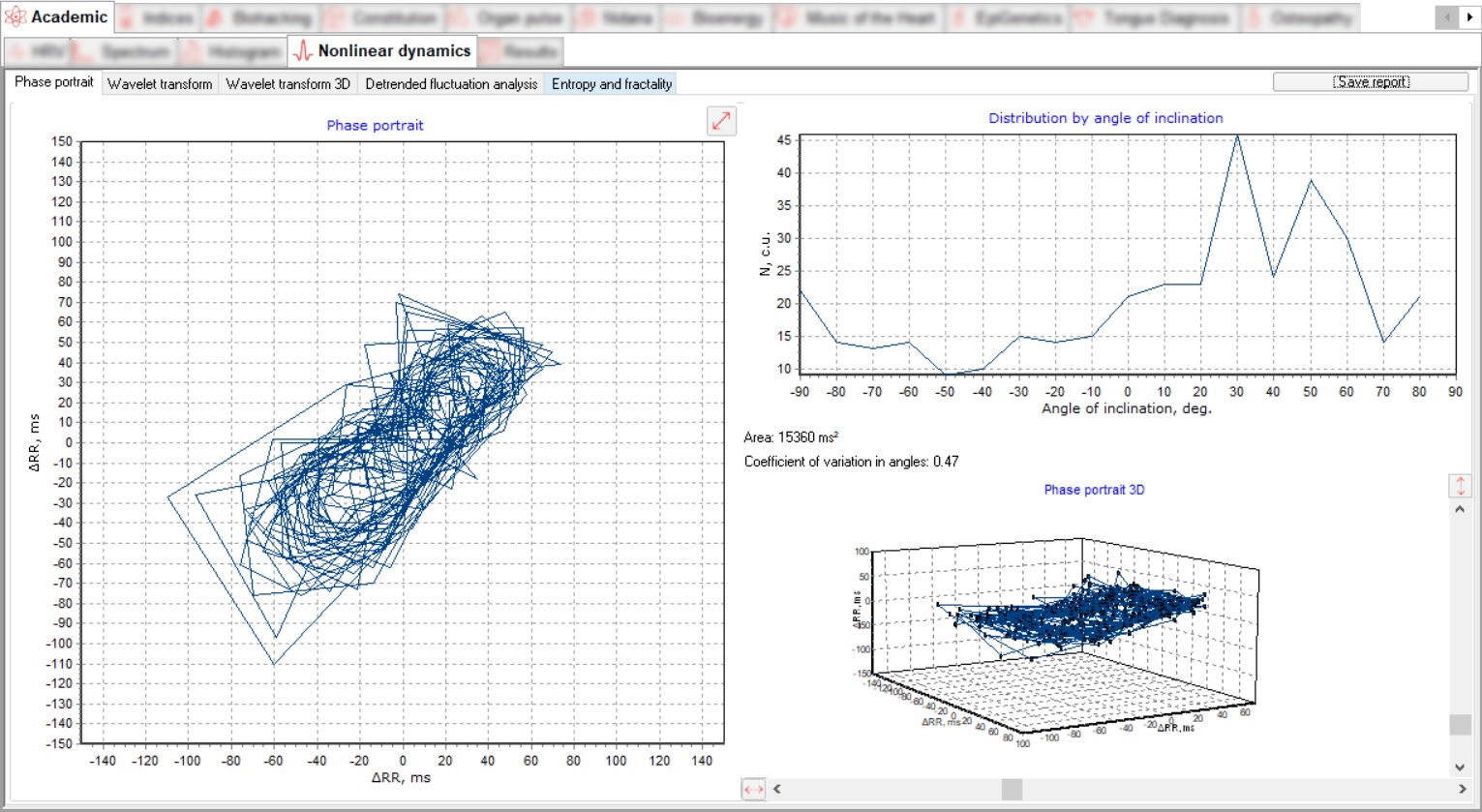
De driehoekige trajecten van het chaosogram duiden op spanning en instabiliteit. Er zijn zones van instabiliteit (ectopische foci) en het systeem springt van één onstabiele toestand naar een andere. Patiënten met acuut coronair syndroom zijn gekenmerkt door dergelijke chaosogrammen, en de meer acute stadia coördineren met de scherpere hoeken van de hoekpunten van de driehoek.

Bij meerdere extrasystolen krijgt het chaosgram een puntig uiterlijk. In boezemfibrilleren, toont het chaosgram lijnen die op een wanordelijke manier zijn getrokken. In patiënten met coronaire hartziekte met cardiosclerose na een infarct, de Het hartritme is stijf, het chaosgram heeft de vorm van een “bagel”.

Chaosogrammen van patiënten met atriumfibrilleren worden gekenmerkt door de vorming van lijnen waarvan de grootte en oriëntatie willekeurig veranderen. Dat heeft geen zin van aantrekkingskracht, wat aangeeft dat het hartritme ongeorganiseerd is.

2 Wavelet Transformeren

De analytische waarde van een dergelijke grafische weergave van het signaal stelt u in staat om Volg zowel veranderingen in tijd als veranderingen in frequentie tegelijkertijd. Deze methode van visualisatie stelt ons in staat om morfologische verschillen tussen ECG te detecteren signalen, evenals mogelijk individuele pieken en segmenten analyseren. De software presenteert de gegevens op een vlak en in een 3D-visualisatie-indeling.

Het ECG-signaal bevindt zich in de coördinaten “vermogen – frequentie – tijd”, waarbij We kunnen de afhankelijkheid van het signaalspectrum op tijd volgen. De tijdsfrequentie weergave van het signaal wordt weergegeven in twee tabbladen, Wavelet Transform en 3D Wavelet Transformeren.

Twee dynamische grafieken tonen de spectrale en temporele ontleding van het signaal.

 

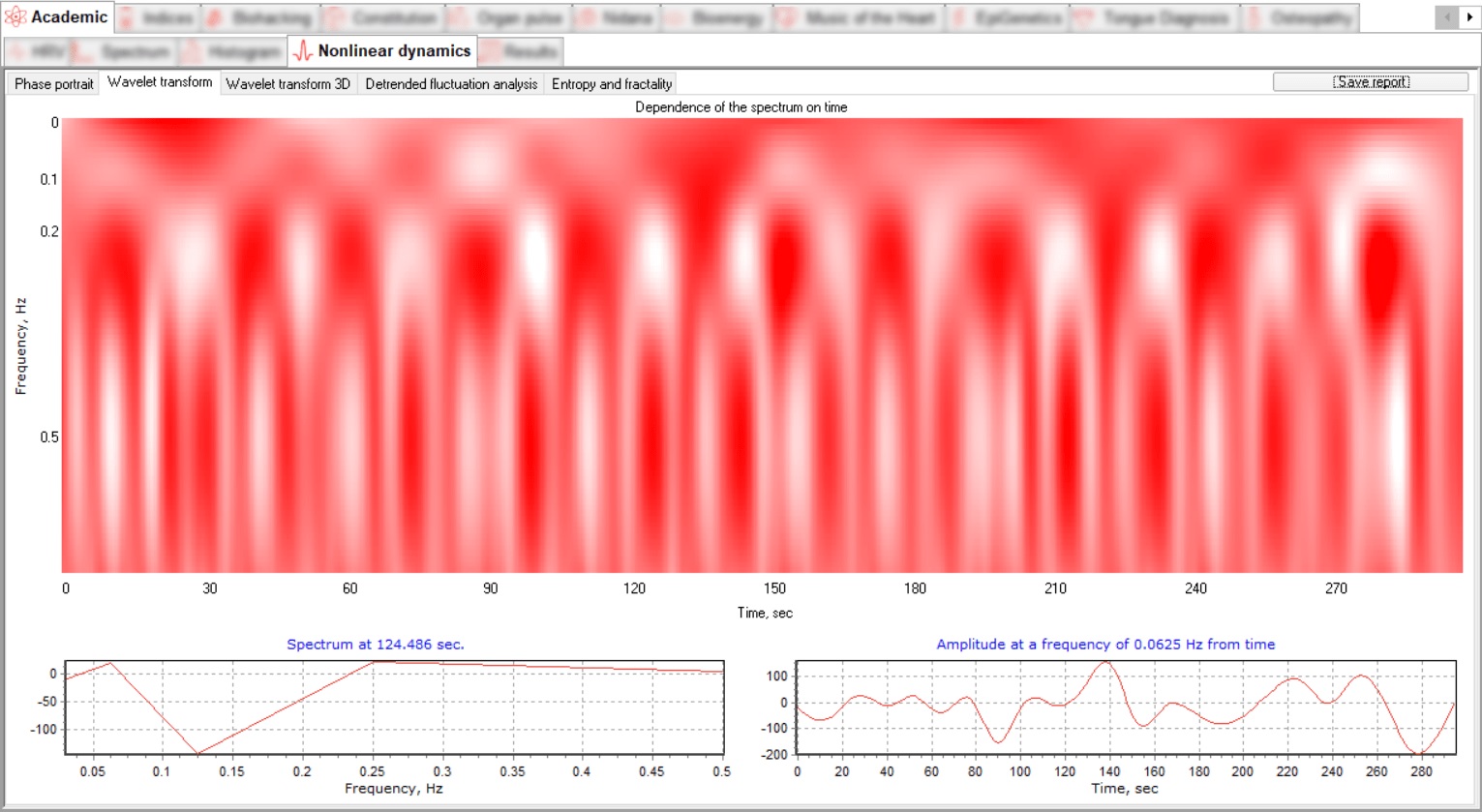
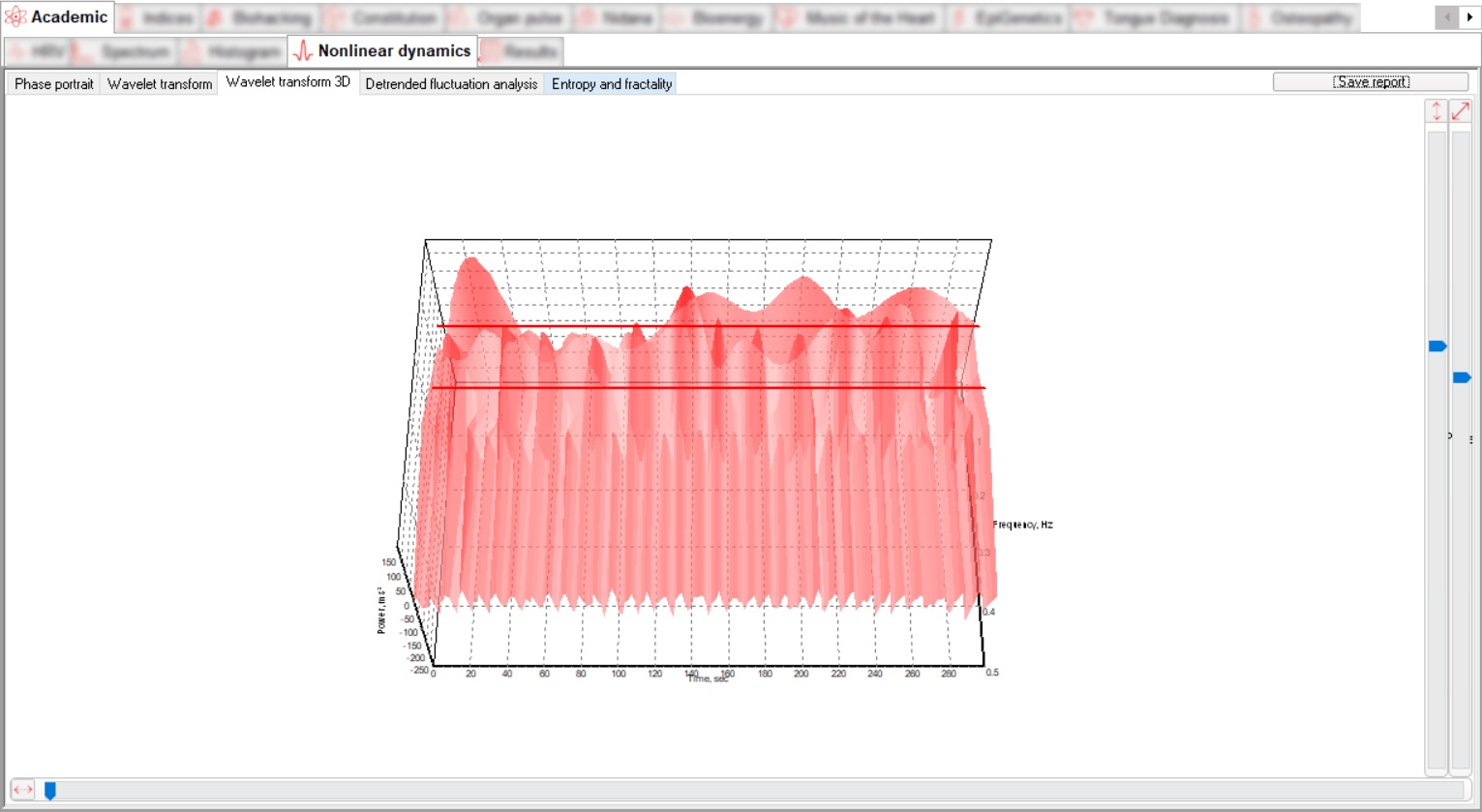
3 Deterende fluctuatie analyse

De α DFA-coëfficiënt kan worden geïnterpreteerd als de ruisindex van de onderliggende waarde dataset. Grotere alfawaarden duiden op een grotere correlatie op verschillende schalen, terwijl kleinere waarden wijzen op minder correlatie en in zekere zin meer chaotische en willekeurige gegevens. DFA-analyse maakt het mogelijk om de zelfgelijkvormigheid te detecteren eigenschappen die inherent zijn aan tijdreeksen en ook om artefacttrends te vermijden.

De hartslag wordt chaotischer naarmate deze wordt blootgesteld aan verhoogde acute stress veroorzaakt door lichamelijke inspanning. De DFA-α daalt bijvoorbeeld onder de 0,75 bij de aerobe drempel en lager dan 0,5 bij de anaerobe drempel.

Detrende Fluctuatie Analyse wordt gepresenteerd in twee grafieken.

 

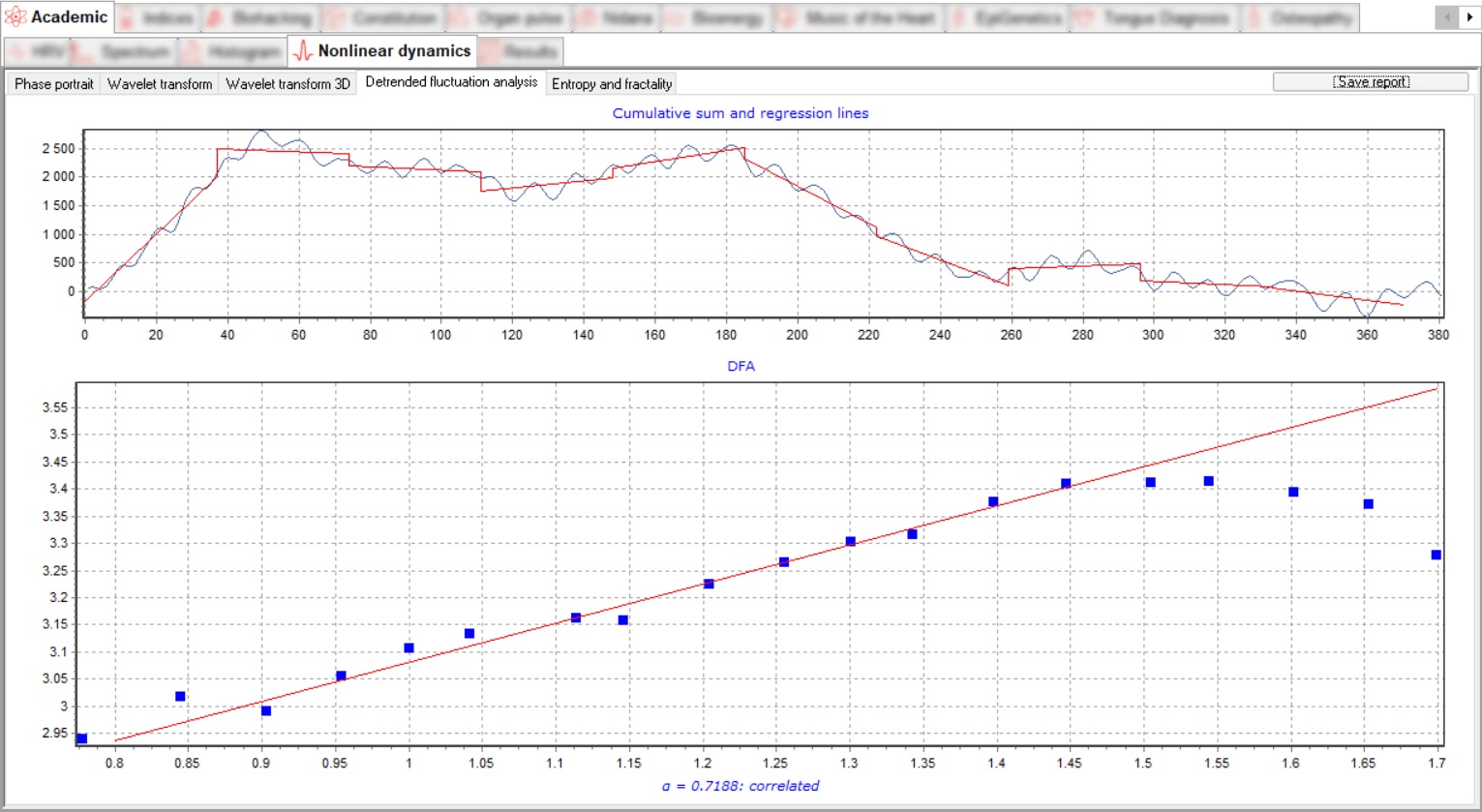
De bovenste grafiek toont de eerste fase in de berekening van de DFA-coëfficiënt α – de cumulatieve som wordt berekend en de belangrijkste trend wordt geïdentificeerd door regressielijnen.

De onderste grafiek toont de punten van afwijking van de regressie op verschillende schalen en de regressielijn erlangs, in logaritmische schalen, de hoek van Helling van de lijn komt overeen met de coëfficiënt α.

4 Entropie en fractaliteit

De fractaldimensie is een indicator van de complexiteit van het proces, waarvan de omvang het mogelijk maakt om het gedrag van het systeem te voorspellen en onstabiele toestanden te diagnosticeren. De toepassing van een niet-lineaire dynamische benadering stelt ons in staat om te beoordelen hoe het studiesysteem functioneert (regelmatig of onregelmatig, en indien onregelmatig, in welke mate) en om de complexiteit van zijn dynamiek te bepalen.

De sectie Entropie en Fractaliteit bevat een grafiek van de analyse van de fractalstructuur van de tijdreeksen in dubbele logaritmische coördinaten en een regressielijn waarvan de helling overeenkomt met de Hurst-indicator.

De Hurst-exponent H wordt gebruikt als maat voor de willekeur van tijdreeksgegevens. Het schat de autocorrelatie van tijdreeksen en de snelheid waarmee deze afneemt met toenemende tijd tussen paren van waarden. Het kwantificeert de relatieve neiging van een tijdreeks om ofwel sterk terug te vallen naar het gemiddelde of om in een bepaalde richting te clusteren.

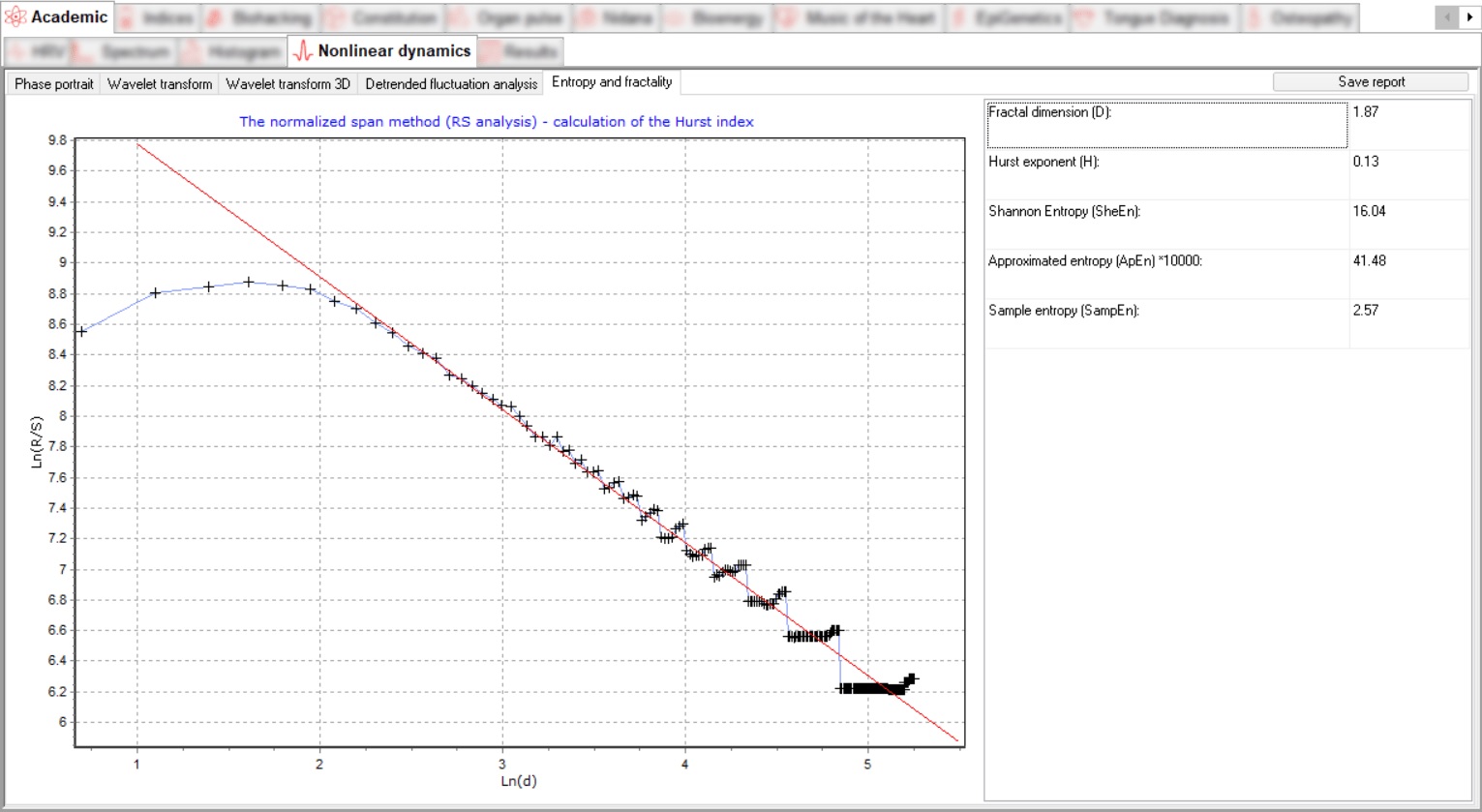
Shannon-entropie drukt de onzekerheid uit in de realisatie van een willekeurige variabele. Entropie is dus het verschil tussen de informatie in het bericht en het deel van de informatie dat precies bekend (of goed voorspelbaar) is in het bericht.

Benaderende entropie (ApEn) karakteriseert de mate van complexiteit van het signaal. Hoe meer uitgesproken de regelmatige component van het signaal, hoe lager de waarde van deze meting, en vice versa.

Een significante afname van entropie gaat meestal gepaard met uitgesproken klinische manifestaties van een negatieve prognose van de ziekte of de negatieve dynamiek ervan. Lage entropie-indicatoren in combinatie met een afname van vagale activiteit begeleiden de nederlaag van het autonome zenuwstelsel bij diabetes mellitus en de vorming van polyneuropathie.

De Sample entropie (SampEn) is een modificatie van de geschatte entropie (ApEn) die wordt gebruikt om de complexiteit van fysiologische tijdreeksen van signalen te schatten die morbide toestanden diagnosticeren.